CBSE Class 11 Maths Notes Chapter 5 Complex Numbers and Quadratic Equations

Imaginary Numbers
The square root of a negative real number is called an imaginary number, e.g. √-2, √-5 etc.
The quantity √-1 is an imaginary unit and it is denoted by ‘i’ called Iota.

Integral Power of IOTA (i)
i = √-1, i² = -1, i³ = -i, i⁴ = 1
So, i⁴ⁿ⁺¹ = i, i⁴ⁿ⁺² = -1, i⁴ⁿ⁺³ = -i, i⁴ⁿ = 1

Note:

• For any two real numbers a and b, the result √a × √b : √ab is true only, when atleast one of the given numbers i.e. either zero or positive.
  √-a × √-b ≠ √ab
  So, i² = √-1 × √-1 ≠ 1
• ‘i’ is neither positive, zero nor negative.
• iⁿ + iⁿ⁺¹ + iⁿ⁺² + iⁿ⁺³ = 0

Complex Number
A number of the form x + iy, where x and y are real numbers, is called a complex number, x is called real part and y is called imaginary part of the complex number i.e. Re(Z) = x and Im(Z) = y.

Purely Real and Purely Imaginary Complex Number
A complex number Z = x + iy is a purely real if its imaginary part is 0, i.e. Im(z) = 0 and purely imaginary if its real part is 0 i.e. Re (z) = 0.

Equality of Complex Number
Two complex numbers z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ are equal, iff x₁ = x₂ and y₁ = y₂ i.e. Re(z₁) = Re(z₂) and Im(z₁) = Im(z₂)
Note: Order relation “greater than’’ and “less than” are not defined for complex number.

Algebra of Complex Numbers
Addition of complex numbers
Let z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ be any two complex numbers, then their sum defined as
z₁ + z₂ = (x₁ + iy₁) + (x₂ + iy₂) = (x₁ + x₂) + i (y₁ + y₂)

Properties of Addition

• Commutative: z₁ + z₂ = z₂ + z₁
• Associative: z₁ + (z₂ + z₃) = (z₁ + z₂) + z₃
• Additive identity z + 0 = z = 0 + z
  Here, 0 is additive identity.

Subtraction of complex numbers
Let z₁ = (x₁ + iy₁) and z₂ = (x₂ + iy₂) be any two complex numbers, then their difference is defined as
z₁ – z₂ = (x₁ + iy₁) – (x₂ + iy₂) = (x₁ – x₂) + i(y₁ – y₂)

Multiplication of complex numbers
Let z₁ = (x₁ + iy₁) and z₂ = (x₂ + iy₂) be any two complex numbers, then their multiplication is defined as
z₁z₂ = (x₁ + iy₁) (x₂ + iy₂) = (x₁x₂ – y₁y₂) + i (x₁y₂ + x₂y₁)

Properties of Multiplication

• Commutative: z₁z₂ = z₂z₁
• Associative: z₁(z₂z₃) = (z₁z₂)z₃
• Multiplicative identity: z . 1 = z = 1 . z
  Here, 1 is multiplicative identity of an element z.
• Multiplicative inverse: For every non-zero complex number z, there exists a complex number z₁ such that z . z₁ = 1 = z₁ . z
• Distributive law: z₁(z₂ + z₃) = z₁z₂ + z₁z₃

Division of Complex Numbers
Let z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂ be any two complex numbers, then their division is defined as

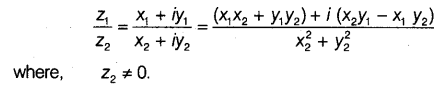
Conjugate of Complex Number
Let z = x + iy, if ‘i’ is replaced by (-i), then said to be conjugate of the complex number z and it is denoted by $\bar { z }$, i.e. $\bar { z }$ = x – iy

Properties of Conjugate

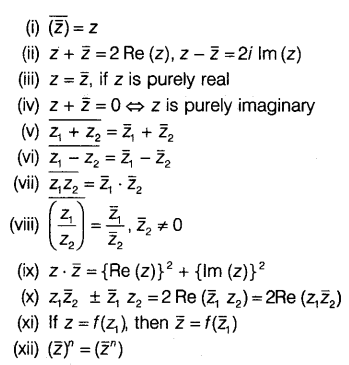
Modulus of a Complex Number
Let z = x + iy be a complex number. Then, the positive square root of the sum of square of real part and square of imaginary part is called modulus (absolute values) of z and it is denoted by |z| i.e. |z| = $\sqrt { { x }^{ 2 }+{ y }^{ 2 } }$
It represents a distance of z from origin in the set of complex number c, the order relation is not defined
i.e. z₁ > z₂ or z₁ < z₂ has no meaning but |z₁| > |z₂| or |z₁|<|z₂| has got its meaning, since |z₁| and |z₂| are real numbers.

Properties of Modulus of a Complex number

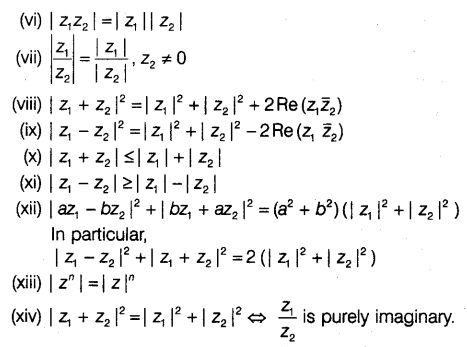
Argand Plane
Any complex number z = x + iy can be represented geometrically by a point (x, y) in a plane, called argand plane or gaussian plane. A purely number x, i.e. (x + 0i) is represented by the point (x, 0) on X-axis. Therefore, X-axis is called real axis. A purely imaginary number iy i.e. (0 + iy) is represented by the point (0, y) on the y-axis. Therefore, the y-axis is called the imaginary axis.

Argument of a complex Number
The angle made by line joining point z to the origin, with the positive direction of X-axis in an anti-clockwise sense is called argument or amplitude of complex number. It is denoted by the symbol arg(z) or amp(z).
arg(z) = θ = tan-1($\frac { y }{ x }$)

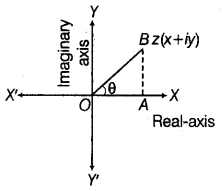
Argument of z is not unique, general value of the argument of z is 2nπ + θ, but arg(0) is not defined. The unique value of θ such that -π < θ ≤ π is called the principal value of the amplitude or principal argument.

Principal Value of Argument

• if x > 0 and y > 0, then arg(z) = θ
• if x < 0 and y > 0, then arg(z) = π – θ
• if x < 0 and y < 0, then arg(z) = -(π – θ)
• if x > 0 and y < 0, then arg(z) = -θ

Polar Form of a Complex Number
If z = x + iy is a complex number, then z can be written as z = |z| (cosθ + isinθ), where θ = arg(z). This is called polar form. If the general value of the argument is θ, then the polar form of z is z = |z| [cos (2nπ + θ) + isin(2nπ + θ)], where n is an integer.

Square Root of a Complex Number

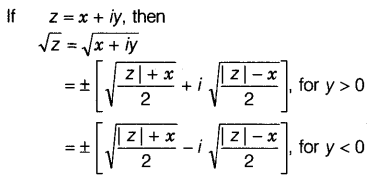
Solution of a Quadratic Equation
The equation ax² + bx + c = 0, where a, b and c are numbers (real or complex, a ≠ 0) is called the general quadratic equation in variable x. The values of the variable satisfying the given equation are called roots of the equation.

The quadratic equation ax² + bx + c = 0 with real coefficients has two roots given by $\frac { -b+\surd D }{ 2a }$ and $\frac { -b-\surd D }{ 2a }$, where D = b² – 4ac, called the discriminant of the equation.

Note:
(i) When D = 0, roots ore real and equal. When D > 0 roots are real and unequal. Further If a,b, c ∈ Q and D is perfect square, then the roots of quadratic equation are real and unequal and if a, b, c ∈ Q and D is not perfect square, then the roots are irrational and occur in pair. When D < 0, roots of the equation are non real (or complex).

(ii) Let α, β be the roots of quadratic equation ax² + bx + c = 0, then sum of roots α + β = $\frac { -b }{ a }$ and the product of roots αβ = $\frac { c }{ a }$.