CBSE Class 11 Maths Notes Chapter 2 Relations and Functions

Ordered Pair
An ordered pair consists of two objects or elements in a given fixed order.

Equality of Two Ordered Pairs
Two ordered pairs (a, b) and (c, d) are equal if a = c and b = d.

Cartesian Product of Two Sets
For any two non-empty sets A and B, the set of all ordered pairs (a, b) where a ∈ A and b ∈ B is called the cartesian product of sets A and B and is denoted by A × B.
Thus, A × B = {(a, b) : a ∈ A and b ∈ B}
If A = Φ or B = Φ, then we define A × B = Φ

Note:

• A × B ≠ B × A
• If n(A) = m and n(B) = n, then n(A × B) = mn and n(B × A) = mn
• If atieast one of A and B is infinite, then (A × B) is infinite and (B × A) is infinite.

Relations
A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product set A × B. The subset is derived by describing a relationship between the first element and the second element of the ordered pairs in A × B.
The set of all first elements in a relation R is called the domain of the relation B, and the set of all second elements called images is called the range of R.

Note:

• A relation may be represented either by the Roster form or by the set of builder form, or by an arrow diagram which is a visual representation of relation.
• If n(A) = m, n(B) = n, then n(A × B) = mn and the total number of possible relations from set A to set B = 2mn

Inverse of Relation
For any two non-empty sets A and B. Let R be a relation from a set A to a set B. Then, the inverse of relation R, denoted by R-1 is a relation from B to A and it is defined by
R-1 ={(b, a) : (a, b) ∈ R}
Domain of R = Range of R-1 and
Range of R = Domain of R-1.

Functions
A relation f from a set A to set B is said to be function, if every element of set A has one and only image in set B.
In other words, a function f is a relation such that no two pairs in the relation have the first element.

Real-Valued Function
A function f : A → B is called a real-valued function if B is a subset of R (set of all real numbers). If A and B both are subsets of R, then f is called a real function.

Some Specific Types of Functions
Identity function: The function f : R → R defined by f(x) = x for each x ∈ R is called identity function.
Domain of f = R; Range of f = R

Constant function: The function f : R → R defined by f(x) = C, x ∈ R, where C is a constant ∈ R, is called a constant function.
Domain of f = R; Range of f = C

Polynomial function: A real valued function f : R → R defined by f(x) = a₀ + a₁x + a₂x²+…+ a_nxⁿ, where n ∈ N and a₀, a₁, a₂,…….. a_n ∈ R for each x ∈ R, is called polynomial function.

Rational function: These are the real function of type $\frac { f(x) }{ g(x) }$, where f(x)and g(x)are polynomial functions of x defined in a domain, where g(x) ≠ 0.

The modulus function: The real function f : R → R defined by f(x) = |x|
or

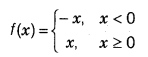
The modulus function: The real function f : R → R defined by f(x) = |x|
or

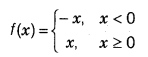
Signum function: The real function f : R → R defined
by f(x) = $\frac { \left| x \right| }{ x }$, x ≠ 0 and 0, if x = 0
or

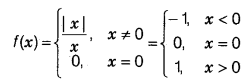
is called the signum function.
Domain of f = R; Range of f = {-1, 0, 1}

Greatest integer function: The real function f : R → R defined by f (x) = {x}, x ∈ R assumes that the values of the greatest integer less than or equal to x, is called the greatest integer function.
Domain of f = R; Range of f = Integer

Fractional part function: The real function f : R → R defined by f(x) = {x}, x ∈ R is called the fractional part function.
f(x) = {x} = x – [x] for all x ∈R
Domain of f = R; Range of f = [0, 1)

Algebra of Real Functions
Addition of two real functions: Let f : X → R and g : X → R be any two real functions, where X ∈ R. Then, we define (f + g) : X → R by
{f + g) (x) = f(x) + g(x), for all x ∈ X.

Subtraction of a real function from another: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, we define (f – g) : X → R by (f – g) (x) = f (x) – g(x), for all x ∈ X.

Multiplication by a scalar: Let f : X → R be a real function and K be any scalar belonging to R. Then, the product of Kf is function from X to R defined by (Kf)(x) = Kf(x) for all x ∈ X.

Multiplication of two real functions: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. Then, product of these two functions i.e. f.g : X → R is defined by (fg) x = f(x) . g(x) ∀ x ∈ X.

Quotient of two real functions: Let f and g be two real functions defined from X → R. The quotient of f by g denoted by $\frac { f }{ g }$ is a function defined from X → R as